Leetcode hot100 回溯
|
541
|
0
|
编程

2632 字
|
17 分钟

全排列

给定一个不含重复数字的数组 nums​ ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入： nums = [1,2,3]
输出： [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

‍

示例 2：

输入： nums = [0,1]
输出： [[0,1],[1,0]]

示例 3：

输入： nums = [1]
输出： [[1]]

题目描述

给定一个不含重复数字的数组 nums​ ，请返回所有可能的全排列。

示例:

  • 输入：[1,2,3]​
  • 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]​

思路

采用回溯法 (Backtracking)：

  1. 定义一个 DFS 函数，通过逐步应用 nums 中的数字构造排列。
  2. 通过 if 条件 item not in output​ 确保各个数字只使用一次，避免重复。
  3. 当构造完整排列后，保存一份副本到结果集合。
  4. 通过 output.pop()​ 完成回退，完成所有路径的遍历。

代码

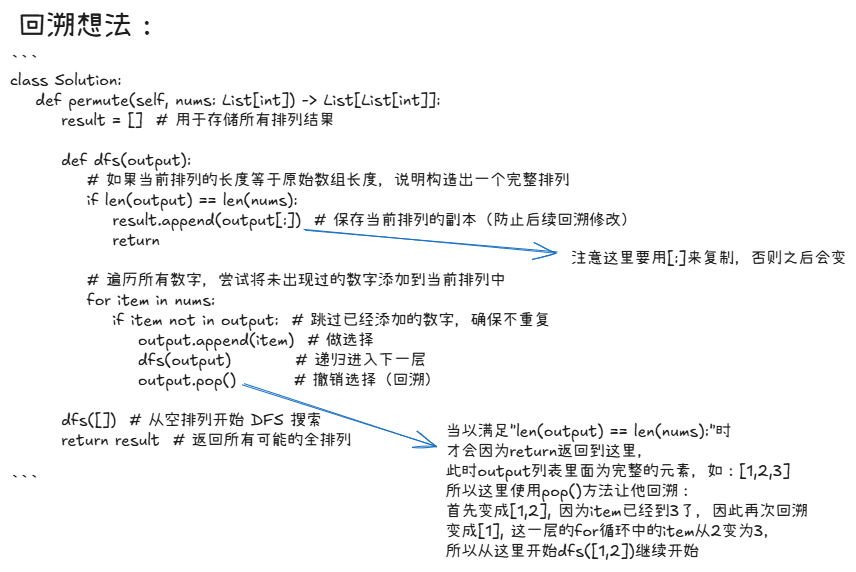
class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        result = []  # 用于存储所有排列结果
        
        def dfs(output):
            # 如果当前排列的长度等于原始数组长度，说明构造出一个完整排列
            if len(output) == len(nums):
                result.append(output[:])  # 保存当前排列的副本（防止后续回溯修改）
                return
            
            # 遍历所有数字，尝试将未出现过的数字添加到当前排列中
            for item in nums:
                if item not in output:  # 跳过已经添加的数字，确保不重复
                    output.append(item)  # 做选择
                    dfs(output)          # 递归进入下一层
                    output.pop()         # 撤销选择（回溯）

        dfs([])  # 从空排列开始 DFS 搜索
        return result  # 返回所有可能的全排列

复杂度

时间复杂度：O(n × n!)​

  • ​n!​ 是排列的总数，每次顺序都需要 O(n)​ 时间处理。

空间复杂度：

  • 不计结果：O(n)​ (最深跳递调用堆栈)
  • 如计入结果：O(n × n!)​

可能的优化

  • 用一个 used​ 标记数组代替 item not in output​，减少 in 操作的运算处理时间
  • 如果有重复元素，需要先排序 + 分支跳过重复

其他

  • 这类问题很適合练习回溯思想和路径遍历
  • 同类题目如：启用组合、N Queens、分组等

思路
​

子集

给你一个整数数组 nums​ ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

**输入：**​nums = [1,2,3]​
**输出：**​[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]​

示例 2：

**输入：**​nums = [0]​
**输出：**​[[],[0]]​

思路一

使用深度优先搜索（DFS）递归遍历的方式，逐步构建子集：

  • 每一层递归表示当前构建的子集。
  • 每次递归都将当前子集 temp​ 加入到结果集中。
  • 遍历从当前索引 index​ 开始，避免重复。
  • 对于每个位置，可以选择加入当前元素或不加入。
  • 使用回溯（在递归返回后弹出最后加入的元素）来恢复现场，继续尝试下一个元素。

Code

from typing import List

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        result = []
        length = len(nums)

        def dfs(temp: List[int], index: int):
            # 将当前子集拷贝一份加入结果
            result.append(temp[:])

            # 从当前位置开始遍历
            for i in range(index, length):
                # 选择当前元素
                temp.append(nums[i])
                # 递归到下一层，索引移动到i+1
                dfs(temp, i + 1)
                # 回溯，撤销选择
                temp.pop()

        dfs([], 0)
        return result

时间空间复杂度

  • 时间复杂度：O(2^n × n)

    • 每个元素有选和不选两种可能，总共 2^n 个子集。
    • 每次生成子集需要 O(n) 的时间拷贝当前 temp​。

  • 空间复杂度：O(2^n × n)

    • 需要存储 2^n 个子集，每个子集最大长度为 n。
    • 递归调用栈最大深度为 n。

注意事项

  • 不要忘记在每一层递归中把当前子集加入到结果集中。
  • 递归时应该传递 i + 1​，防止同一元素被多次使用。
  • 使用回溯的思想（递归后 pop​），避免破坏当前子集。
  • 不需要提前剪枝到固定长度，因为子集可以是任意长度。

错误反思

  • 初版代码中错误地以子集长度为终止条件，导致遗漏合法子集。
  • 循环过程中每次 not in temp​ 检查，效率低且不必要。
  • 遍历时未控制好起点，容易导致重复或顺序混乱。
  • 递归时忘记推进索引 (i+1​)，导致元素重复使用。

关键点

  • 每层都记录一次当前子集。
  • 控制遍历起点，防止重复。
  • 回溯撤销选择，保证递归路径正确。
  • 正确理解子集的定义：包括空集和所有元素任意组合的集合。

思路二

采用 DFS + 回溯 方法进行子集生成：

  • 对于数组中的每一个元素，都有两个决策分支：

    1. 不选当前元素，直接进入下一层递归；
    2. 选当前元素，将其加入当前路径 path​，然后继续递归。

  • 当递归到数组末尾（即 index == length​）时，将当前 path​ 的副本保存到结果集中。

  • 通过回溯（path.pop()​），撤销最近的选择，确保不同路径的独立性。

这种方法构建了一棵二叉决策树，系统地穷举出所有子集。

整体 DFS 树形结构

dfs(0) path = []
├── 不选 1 → dfs(1) path = []
│   ├── 不选 2 → dfs(2) path = []
│   │   ├── 不选 3 → dfs(3) path = [] → 收集 []
│   │   └── 选 3 → dfs(3) path = [3] → 收集 [3] 
│   │       (回溯 pop -> path = [])
│   └── 选 2 → dfs(2) path = [2]
│       ├── 不选 3 → dfs(3) path = [2] → 收集 [2]
│       └── 选 3 → dfs(3) path = [2,3] → 收集 [2,3]
│           (回溯 pop -> path = [2])
│       (回溯 pop -> path = [])
├── 选 1 → dfs(1) path = [1]
│   ├── 不选 2 → dfs(2) path = [1]
│   │   ├── 不选 3 → dfs(3) path = [1] → 收集 [1]
│   │   └── 选 3 → dfs(3) path = [1,3] → 收集 [1,3]
│   │       (回溯 pop -> path = [1])
│   └── 选 2 → dfs(2) path = [1,2]
│       ├── 不选 3 → dfs(3) path = [1,2] → 收集 [1,2]
│       └── 选 3 → dfs(3) path = [1,2,3] → 收集 [1,2,3]
│           (回溯 pop -> path = [1,2])
│       (回溯 pop -> path = [1])
│   (回溯 pop -> path = [])

Code

from typing import List

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        result = []
        path = []
        length = len(nums)

        def dfs(index: int):
            # 当所有元素处理完毕时，记录当前路径
            if index == length:
                result.append(path[:])
                return
            
            # 分支一：不选择当前元素
            dfs(index + 1)

            # 分支二：选择当前元素
            path.append(nums[index])
            dfs(index + 1)
            
            # 回溯，撤销选择
            path.pop()

        dfs(0)
        return result

时间空间复杂度

  • 时间复杂度：O(2^n)

    • 每个元素有两种选择（选或不选），总共有 2^n 种子集。
    • 这里每个子集的构建操作是常数级别的，且 path​ 的拷贝操作均匀分布在树的叶子节点，因此总复杂度为 O(2^n)。

  • 空间复杂度：

    • 递归栈空间：O(n)，最深递归深度为 n。
    • 结果集空间：O(2^n × n)，存储所有子集及其元素。

注意事项

  • 递归过程中，每到叶子节点（即 index == length）时，需要拷贝一份 path​ 加入结果。
  • 必须在每次递归结束后执行 回溯（​​path.pop()​ ​ ） ，撤销之前的选择，保持路径干净，避免不同子集间互相干扰。
  • 每次选择和不选择当前元素，都要继续递归，不遗漏任何一种情况。

错误反思

  • 初期可能容易漏掉「不选当前元素」的分支，只考虑了添加元素的情况。
  • 也容易忘记在添加元素后，需要在递归回来时执行 pop()​，否则导致路径累积错误。
  • 忽略拷贝 path[:]​ 而直接 append path，会导致结果中所有子集共享同一个 path（动态变化），最终结果错误。

关键点

  • 二叉决策树建模：每个元素的选与不选构成了二叉树结构。
  • 回溯操作：确保每一条路径独立探索。
  • 状态保存：在递归结束点，拷贝当前路径保存子集。
  • 时间与空间的指数增长：符合所有子集生成的复杂度要求，无法进一步降低。

总结

这是一种非常简洁且高效的子集生成方法，通过系统地决策每一个元素是否加入，配合回溯，能够穷举出所有子集，同时代码结构清晰，便于理解和扩展。

电话号码的字母组合

给定一个仅包含数字 2-9​ 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

200px-telephone-keypad2svg

示例 1：

**输入：**​digits = "23"​
**输出：**​["ad","ae","af","bd","be","bf","cd","ce","cf"]​

示例 2：

**输入：**​digits = ""​
**输出：**​[]​

示例 3：

**输入：**​digits = "2"​
**输出：**​["a","b","c"]​

‍

思路

使用DFS + 回溯方法：

  • 对于 digits​ 中的每一个数字，根据数字映射到对应的字符集合。
  • 每一层递归，枚举当前数字可能对应的每一个字母，加入到临时路径 temp​。
  • 每次递归到底（即所有数字都处理完了，i == length​），将 temp​ 中的字符组合成字符串加入 result​。
  • 使用回溯（temp.pop()​）撤销最近的选择，保证每条路径独立探索。

Code

from typing import List

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if digits == "":
            return []

        # 数字到字母的映射表
        phone_dict = {
            '2': ['a', 'b', 'c'],
            '3': ['d', 'e', 'f'],
            '4': ['g', 'h', 'i'],
            '5': ['j', 'k', 'l'],
            '6': ['m', 'n', 'o'],
            '7': ['p', 'q', 'r', 's'],
            '8': ['t', 'u', 'v'],
            '9': ['w', 'x', 'y', 'z']
        }

        result = []
        temp = []
        length = len(digits)

        def dfs(i: int):
            # 如果处理完所有数字，加入结果
            if i == length:
                result.append(''.join(temp))
                return

            # 遍历当前数字对应的所有字母
            for c in phone_dict[digits[i]]:
                temp.append(c)   # 做选择
                dfs(i + 1)       # 递归处理下一个数字
                temp.pop()       # 撤销选择，回溯

        dfs(0)
        return result

时间空间复杂度

  • 时间复杂度：O(3^n × 4^m)

    • 其中 n 是输入中数字是 2,3,4,5,6,8 的个数（每个对应3个字母），m 是数字是 7,9 的个数（每个对应4个字母）。
    • 总共需要遍历所有可能的组合。

  • 空间复杂度：

    • 递归栈：最多 O(n)，n 是 digits 长度。
    • 结果集：需要 O(3^n × 4^m × n) 的空间保存所有组合。

注意事项

  • 记得处理输入为空字符串的情况，直接返回 []​。
  • 每次递归到底，需要把 temp​ 转成字符串后加入结果。
  • 在递归后回溯 (pop​) 是关键步骤，否则会导致路径混乱。
  • ​phone_dict​ 需要完整且准确，不要漏掉 7 和 9 多一个字母的情况。

错误反思

  • phone_dict初始化错误：

    • 一开始尝试用循环动态生成映射，但由于数字7和9对应4个字母，导致映射表错误。
    • 正确做法是手动完整定义每个数字对应的字母。

  • 添加结果时错误使用了​​temp[:]​ ​而不是字符串：

    • 初版在递归到叶子节点时，直接 result.append(temp[:])​。
    • 这样加入的是一个字符列表（如 ['a', 'd']​），而题目要求是字符串（如 "ad"​）。
    • 正确做法是使用 ''.join(temp)​ 把字符数组拼接成一个整体字符串后再添加到 result​。

  • 笔误导致变量错误：

    • 在早期版本中，将 temp​ 错写成 tem​，导致运行时报错 NameError​。

  • 忽略特殊输入情况：

    • 初版没有在一开始判断 digits == ""​，可能导致不必要的递归调用。
    • 应该在一开始就拦截空输入，直接返回空列表。

关键点

  • 回溯（Backtracking）：每次选择后探索，探索完后撤销选择。
  • 正确处理边界情况：如空字符串。
  • 正确理解并初始化数字到字母的映射表。
  • 理解结果是所有可能组合，不是排列，不是子集，必须遍历完整的组合树。

‍

Leetcode编程
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
2 LeetCode 热题 100 (图论)

							
							

							
9.1 LeetCode 热题 100 (图论)

							
							

							
8.1 LeetCode 热题 100 (二叉树)

							
							

							
7.4 LeetCode 热题 100 (链表)

							
							

							
7.3 LeetCode 热题 100 (链表)