线性量化 Linear quantization
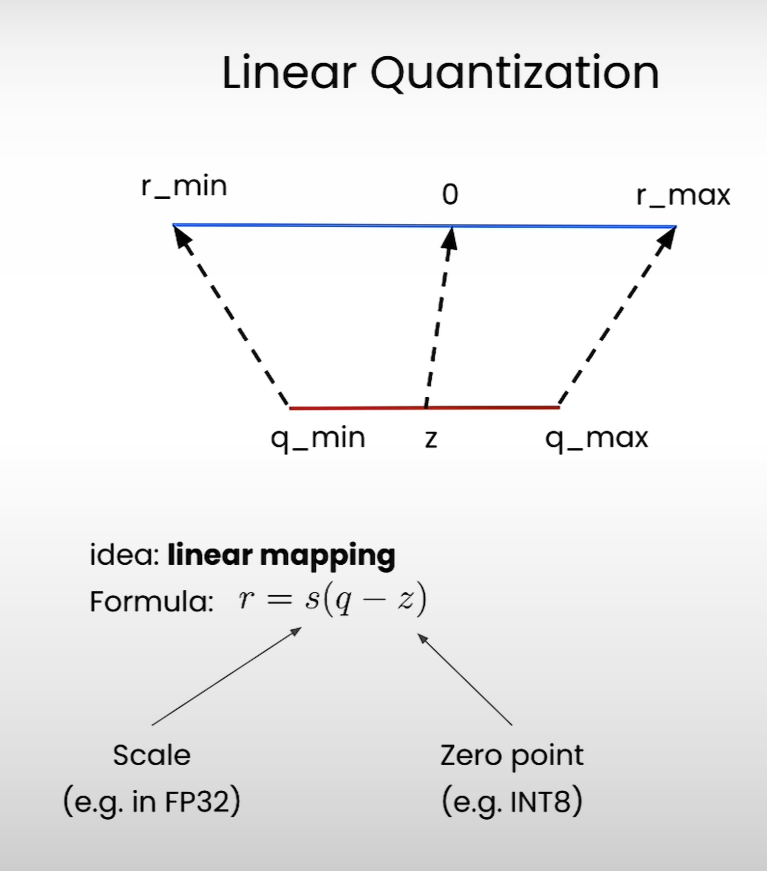
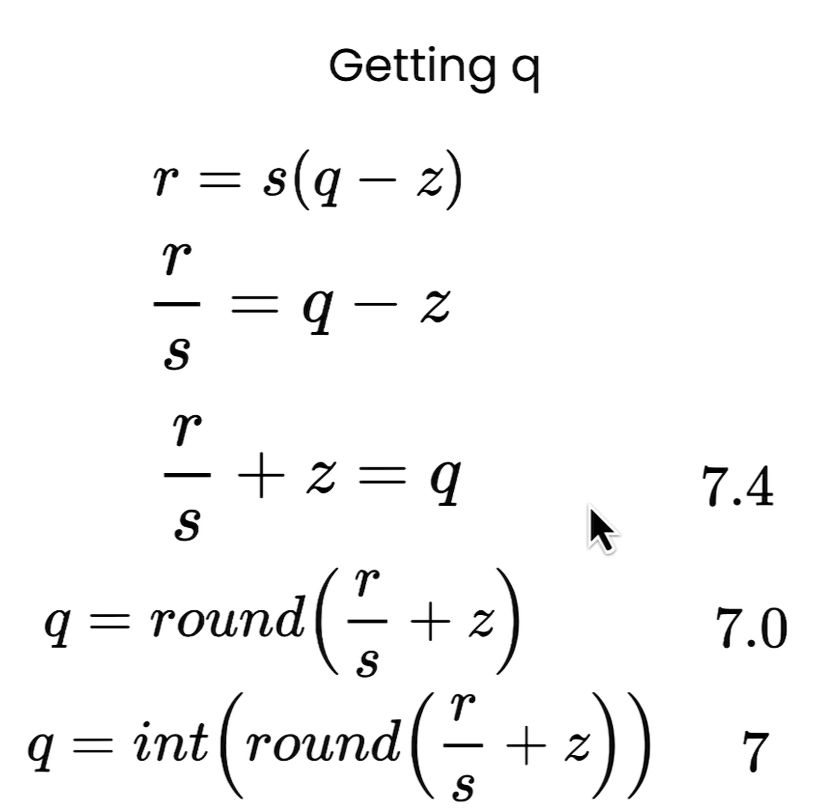
零点 $z$ zero point
缩放因子scaling factor

量化权重或者激活值
对称与不对称量化
1. 对称量化 (Symmetric Quantization)
定义
量化区间关于 0 对称:
$$r \in [-r_{\max}, r_{\max}]
\quad \longrightarrow \quad
q \in [q_{\min}, q_{\max}]$$
- 这里 $r_{\max} = \max(|r_{\min}|, |r_{\max}|)$
- Zero point 固定为 0,不需要平移
- 公式:
$$scale = \frac{r_{\max}}{q_{\max}}
\quad , \quad
q = \text{clamp}\Big(\text{round}(r/scale), q_{\min}, q_{\max}\Big)$$
特点
-
优点
- 简单,硬件实现高效(只需要乘除,不需要加减 zero point)
- 常用于 权重量化,因为权重一般是零均值分布
-
缺点
- 如果数据分布偏移严重(比如 [0, 10]),零点=0 强行对称,区间利用率低
2. 非对称量化 (Asymmetric Quantization)
定义
量化区间不对称,允许浮点范围 [r_min, r_max] 映射到 [q_min, q_max],并通过 zero point 来对齐 0。
- 公式:
$$scale = \frac{r_{\max} – r_{\min}}{q_{\max} – q_{\min}}$$$$zero\_point = \text{round}\Big(q_{\min} – \frac{r_{\min}}{scale}\Big)$$$$q = \text{clamp}\Big(\text{round}(r/scale + zero\_point), q_{\min}, q_{\max}\Big)$$
特点
-
优点
- 区间利用率高,适合分布偏移的激活值(比如 ReLU 输出 ∈ [0, +∞))
- 能精确对齐 0 → 避免 ReLU 层出问题
-
缺点
- 计算复杂,需要额外加减 zero point
- 对硬件更不友好
Per-Channel Quantization (逐通道量化)
定义
- 每个 卷积通道(通常是输出通道)独立计算
scale 和zero_point - 公式:
$$scale_c = \frac{r_{\max,c} – r_{\min,c}}{q_{\max} – q_{\min}}$$$$zero\_point_c = \text{round}\Big(q_{\min} – \frac{r_{\min,c}}{scale_c}\Big)$$
直观理解
- 对于 Conv2D,权重张量形状是
[out_channels, in_channels, kH, kW] - 每个
out_channel 一组参数,就有一个独立的(scale, zero_point)
优点
- 更精细:不同通道的数值范围差异不会互相干扰
- 大幅提升模型精度(尤其是 int8 权重量化)
- 是 PyTorch / TensorRT 等框架里 常用默认设置
缺点
- 存储开销:需要保存每个通道的 scale/zero_point
- 硬件支持要求更高(矩阵乘法时要考虑逐通道缩放)
Per-Group Quantization (逐组量化)
定义
- 折中做法:把多个通道分成一组(比如 4 个或 8 个),每组共享一个
(scale, zero_point) - 公式类似 per-channel,只是统计的是 group 内所有通道的范围
优点
- 精度比 per-tensor 好
- 存储和计算比 per-channel 更省(scale/zero_point 数量少)
- 适合在一些硬件上做优化(如 GPU/TPU 上向量化计算)
缺点
- 比 per-channel 稍微损失一些精度
线性量化后的推理
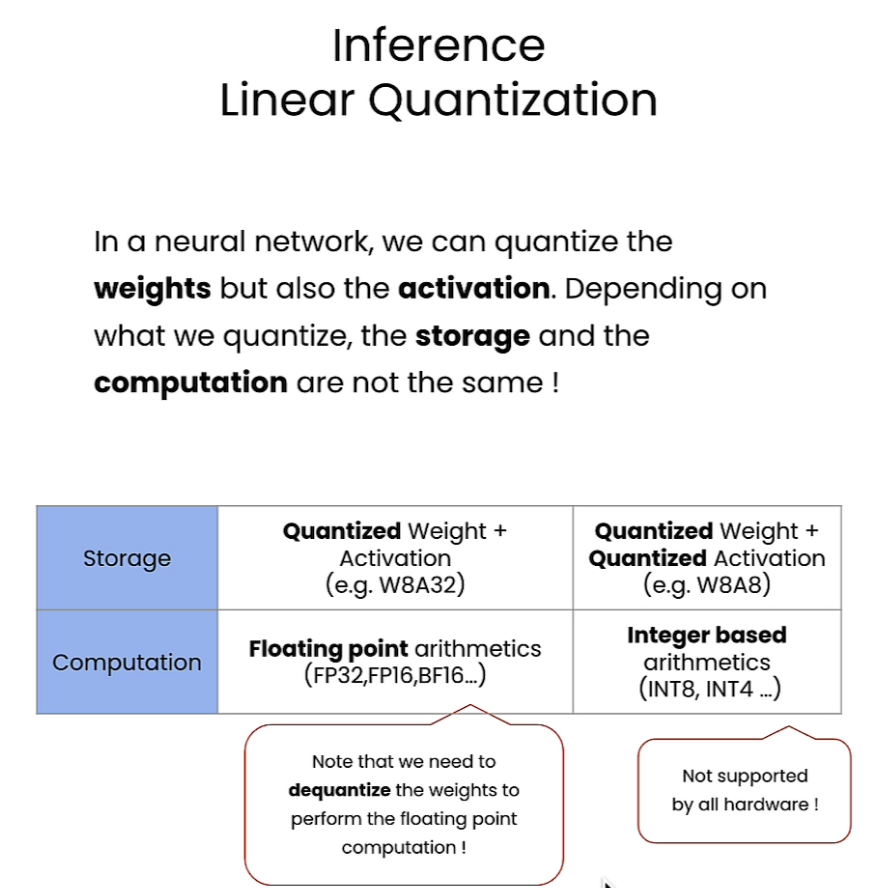
1. 背景
在神经网络推理中,我们既可以量化 权重 (weights) ,也可以量化 激活 (activations) 。
- 权重量化:减少模型存储大小(比如从 FP32 → int8)。
- 激活量化:进一步减少推理时的计算复杂度和内存占用。
不同的量化方式会导致 存储 (storage) 和 计算 (computation) 的方式不同。
2. 左边这一列:权重量化 + 浮点激活 (e.g. W8A32)
-
存储:权重存成 int8(压缩了模型大小),激活仍然用 FP32(或 FP16/BF16)。
-
计算:因为激活还是浮点数 → 计算时必须把权重 反量化 (dequantize) 回浮点数,再和激活做浮点计算。
-
特点:
- 节省了权重存储空间(模型更小)。
- 但计算还是浮点运算,速度提升有限。
- 对硬件支持要求低,几乎所有 GPU/CPU 都能做。
👉 常见在 权重量化推理 (Post-Training Weight Quantization) 中使用。
3. 右边这一列:权重量化 + 激活量化 (e.g. W8A8)
-
存储:权重和激活都存成 int8。
-
计算:直接用 整数算术 (integer arithmetic, INT8/INT4) 做矩阵乘法,速度更快,能显著降低功耗。
-
特点:
- 节省存储(权重和激活都变小)。
- 计算效率最高(真正的低精度加速)。
- 但是:不是所有硬件都支持(比如老 GPU 可能不支持 int8 gemm)。
👉 常见在 全量化推理 (Full INT8 Inference) 中使用,典型如 TensorRT、TPU 上的加速。
4. 图中的两条注释
-
左边:"Note that we need to dequantize the weights to perform the floating point computation!"
- 意思是:如果激活还是 FP32,那权重虽然存成 int8,但用的时候必须还原回浮点数 → 计算其实没加速多少。
-
右边:"Not supported by all hardware!"
- 意思是:真正的 int8/int4 矩阵乘法需要硬件原生支持,不是所有 CPU/GPU/加速器都能做到。
5. 总结对比表
| 方案 | 存储 | 计算 | 优点 | 缺点 |
|---|---|---|---|---|
| W8A32 (权重量化, 激活浮点) | 权重小,激活大 | 浮点运算 (FP32/FP16) | 节省模型大小,兼容性好 | 速度提升有限 |
| W8A8 (权重+激活量化) | 权重小,激活小 | 整数运算 (INT8/INT4) | 存储+速度双优化 | 硬件要求高 |
🔑 一句话总结:
- 只量化权重 (W8A32) → 模型更小,但计算还是浮点 → 节省存储,不一定提速。
- 权重和激活都量化 (W8A8) → 模型更小,计算也更快 → 真正的端到端加速,但需要硬件支持。