7.4 LeetCode 热题 100 (链表)
|
14
|
0
|
编程

1957 字
|
11 分钟

随机链表的复制

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

  • val：一个表示 Node.val 的整数。
  • random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码 只 接受原链表的头节点 head 作为传入参数。

示例 1：

e1

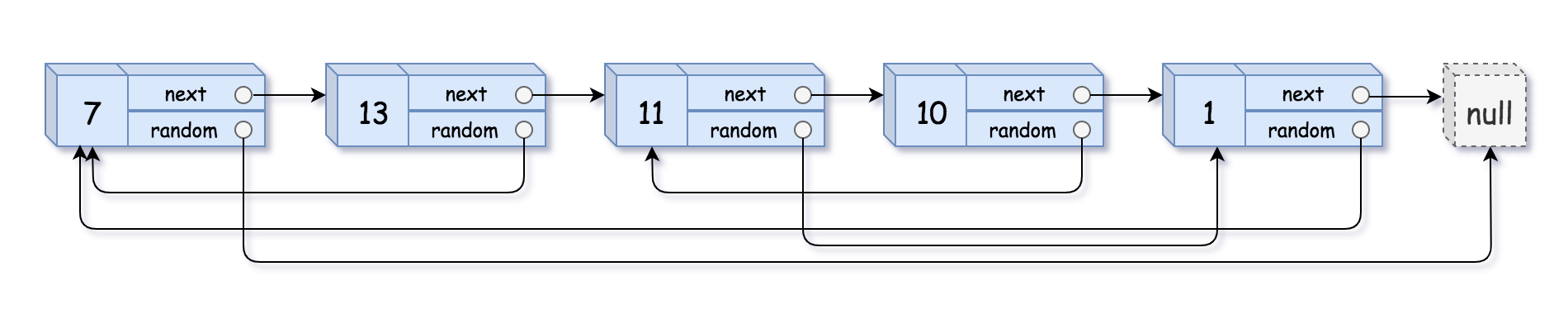
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

e2

输入：head = [[1,1],[2,1]] 输出：[[1,1],[2,1]]

示例 3：

e3

输入：head = [[3,null],[3,0],[3,null]] 输出：[[3,null],[3,0],[3,null]]

方法一: 哈希表

思路

1. 边界检查：

  • 如果链表为空，直接返回 None。

2. 第一遍：复制节点并建立映射：

  • 遍历链表，逐个复制节点并建立 node_dict映射关系：
    • key: 原链表的节点。
    • value: 对应的新链表节点。
  • 同时建立新链表的 next 链接。

3. 第二遍：复制 random 指针：

  • 再次遍历原链表，使用 node_dict 快速找到对应的新链表节点，设置 random 指针。

4. 返回结果：

  • 返回新链表的头节点 new_head。

代码

class Solution:
    def copyRandomList(self, head: 'Optional[Node]') -> 'Optional[Node]':
        if not head:  # 如果链表为空，直接返回 None
            return None

        # 第一遍：复制节点并建立映射关系
        node_dict = {}
        cur = head
        new_head = Node(cur.val)
        node_dict[cur] = new_head
        new_cur = new_head

        while cur.next:
            next_node = Node(cur.next.val)  # 创建新节点
            new_cur.next = next_node       # 建立 next 链接
            node_dict[cur.next] = next_node  # 记录原节点与新节点的映射
            cur = cur.next
            new_cur = new_cur.next

        # 第二遍：处理 random 指针
        cur = head
        new_cur = new_head
        while cur:
            if cur.random:  # 如果当前节点的 random 指针非空
                new_cur.random = node_dict[cur.random]  # 设置新链表的 random
            cur = cur.next
            new_cur = new_cur.next

        return new_head  # 返回新链表的头节点
Python





复杂度





    

  1. 时间复杂度：O(n)

      

    • 第一遍遍历链表 O(n) 复制节点并建立映射。
      • 




    • 第二遍遍历链表 O(n) 复制 random 指针。
      • 




    • 总复杂度为 O(n)。
      • 

    

    2. 




  2. 空间复杂度：O(n)

      

    • 使用了一个字典存储原链表节点到新链表节点的映射，额外占用 O(n)O(n)O(n) 空间。
      • 

    

    3. 






优化点





如果需要优化空间复杂度，可以采用“链表节点插入法”（即将新节点直接插入到原节点后），实现 O(1) 空间复杂度的解决方案。





方法二: 拼接 + 拆分





思路





第一步：插入新节点：





    

  • 在每个原节点后插入一个复制节点，形成交替结构： rust复制代码原链表：1 -> 2 -> 3
     插入后：1 -> 1′ -> 2 -> 2′ -> 3 -> 3′
    • 






第二步：设置 random 指针：





    

  • 利用插入后的交替结构，直接访问 cur.random.next 来设置新节点的 random： 1′.random = 1.random.next
    • 






第三步：分离链表：





    

  • 通过 cur.next 恢复原链表。
    • 




  • 通过 new_cur.next 分离出复制链表。
    • 






分离后：





 原链表：1 -> 2 -> 3
 复制链表：1' -> 2' -> 3'





处理链表末尾：





    

  • 在最后一个节点时，直接处理 cur.next 和 new_cur.next，避免出现 AttributeError。
    • 






代码





class Solution:
    def copyRandomList(self, head: 'Optional[Node]') -> 'Optional[Node]':
        if head is None:  # 如果链表为空，直接返回 None
            return None

        # 第一遍：在原链表中插入新节点
        cur = head
        while cur:
            temp = cur.next
            cur.next = Node(cur.val, temp)
            cur = temp

        # 第二遍：设置新节点的 random 指针
        cur = head
        while cur:
            if cur.random:
                cur.next.random = cur.random.next
            cur = cur.next.next

        # 第三遍：将新链表与原链表分离
        cur = head
        new_head = head.next  # 新链表的头节点
        new_cur = new_head

        while cur:
            cur.next = cur.next.next  # 恢复原链表
            if new_cur.next:  # 更新新链表的 next
                new_cur.next = new_cur.next.next
            cur = cur.next
            new_cur = new_cur.next

        return new_head

Python










你的代码使用的是链表节点插入法，来复制带随机指针的链表。这种方法的空间复杂度为 O(1)O(1)O(1)，非常高效。然而，在最后一步将两个链表分开时，代码逻辑存在一些问题，需要调整。










问题分析





    

  1. 分离链表的逻辑有误：

      

    • 在以下代码段： python复制代码cur = cur.next.next
       next_new_cur = new_cur.next.next
       new_cur.next = next_new_curcur.next.next 和 new_cur.next.next 可能会在最后一个节点上引发 AttributeError，因为链表末尾的 next 是 None。
      • 




    • 同时，分离链表时逻辑不够简洁，可以通过更直接的方式实现。
      • 

    

    2. 




  2. 代码结构优化：

      

    • 在链表分离逻辑中可以减少冗余判断，并直接处理边界条件。
      • 

    

    3. 











改进后的代码





python复制代码class Solution:
    def copyRandomList(self, head: 'Optional[Node]') -> 'Optional[Node]':
        if head is None:  # 如果链表为空，直接返回 None
            return None

        # 第一遍：在原链表中插入新节点
        cur = head
        while cur:
            temp = cur.next
            cur.next = Node(cur.val, temp)
            cur = temp

        # 第二遍：设置新节点的 random 指针
        cur = head
        while cur:
            if cur.random:
                cur.next.random = cur.random.next
            cur = cur.next.next

        # 第三遍：将新链表与原链表分离
        cur = head
        new_head = head.next  # 新链表的头节点
        new_cur = new_head

        while cur:
            cur.next = cur.next.next  # 恢复原链表
            if new_cur.next:  # 更新新链表的 next
                new_cur.next = new_cur.next.next
            cur = cur.next
            new_cur = new_cur.next

        return new_head
Python















改进点说明





    

  1. 第一步：插入新节点：

      

    • 在每个原节点后插入一个复制节点，形成交替结构： rust复制代码原链表：1 -> 2 -> 3
       插入后：1 -> 1′ -> 2 -> 2′ -> 3 -> 3′
      • 

    

    2. 




  2. 第二步：设置 random 指针：

      

    • 利用插入后的交替结构，直接访问 cur.random.next来设置新节点的 random： 1′.random = 1.random.next
      • 

    

    3. 




  3. 第三步：分离链表：
    • 通过 cur.next 恢复原链表。
    • 通过 new_cur.next 分离出复制链表。
    分离后： rust复制代码原链表：1 -> 2 -> 3
     复制链表：1′ -> 2′ -> 3′
    4. 




  4. 处理链表末尾：

      

    • 在最后一个节点时，直接处理 cur.next 和 new_cur.next，避免出现 AttributeError。
      • 

    

    5. 











复杂度





    

  1. 时间复杂度：O(n)

      

    • 每个节点被遍历三次：插入新节点、设置 random 指针、分离链表。
      • 




    • 总时间复杂度为 O(n)。
      • 

    

    2. 




  2. 空间复杂度：O(1)

      

    • 不使用额外的存储结构，只操作链表本身。
      • 

    

    3. 











排序链表





给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。





示例 1：





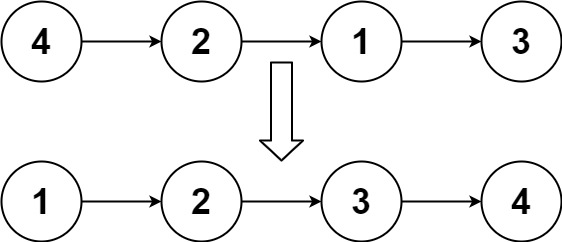
sort_list_1





 输入：head = [4,2,1,3]
 输出：[1,2,3,4]





示例 2：





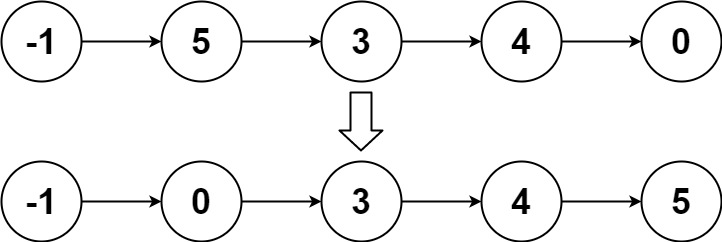
sort_list_2





 输入：head = [-1,5,3,4,0]
 输出：[-1,0,3,4,5]





示例 3：





 输入：head = []
 输出：[]










方法一： 归并排序





思路分析





    

  1. 拆分链表：

      

    • 使用 middleNode 函数，采用快慢指针找到链表的中点，并将链表分成两部分。slow 是中点前的节点，slow.next 被断开，实现链表的拆分。
      • 

    

    2. 




  2. 递归排序：

      

    • 对两个子链表分别调用 sortList 进行递归排序，直到链表长度为 1（递归基）。
      • 

    

    3. 




  3. 合并两个有序链表：

      

    • 使用 mergeTwoLists 函数合并两个已排序的子链表，构建有序链表。
      • 

    

    4. 






代码





class Solution:
    # 876. 链表的中间结点（快慢指针）
    def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
        slow = fast = head
        # 先找到链表的中间结点的【前一个节点】
        while fast.next and fast.next.next:
            slow = slow.next
            fast = fast.next.next
        mid = slow.next  # 下一个节点就是链表的中间结点 mid
        slow.next = None  # 断开 mid 的前一个节点和 mid 的连接
        return mid

    # 21. 合并两个有序链表（双指针）
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        cur = dummy = ListNode()  # 用哨兵节点简化代码逻辑
        while list1 and list2:
            if list1.val < list2.val:
                cur.next = list1  # 把 list1 加到新链表中
                list1 = list1.next
            else:  # 注：相等的情况加哪个节点都是可以的
                cur.next = list2  # 把 list2 加到新链表中
                list2 = list2.next
            cur = cur.next
        cur.next = list1 if list1 else list2  # 拼接剩余链表
        return dummy.next

    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 如果链表为空或者只有一个节点，无需排序
        if head is None or head.next is None:
            return head
        # 找到中间节点，并断开 head2 与其前一个节点的连接
        # 比如 head=[4,2,1,3]，那么 middleNode 调用结束后 head=[4,2] head2=[1,3]
        head2 = self.middleNode(head)
        # 分治
        head = self.sortList(head)
        head2 = self.sortList(head2)
        # 合并
        return self.mergeTwoLists(head, head2)
Python










你的代码实现了基于递归的归并排序来对链表进行排序。以下是代码的思路、时间复杂度分析以及需要优化或注意的点。










思路分析





    

  1. 拆分链表：

      

    • 使用 middleNode 函数，采用快慢指针找到链表的中点，并将链表分成两部分。slow 是中点前的节点，slow.next 被断开，实现链表的拆分。
      • 

    

    2. 




  2. 递归排序：

      

    • 对两个子链表分别调用 sortList 进行递归排序，直到链表长度为 1（递归基）。
      • 

    

    3. 




  3. 合并两个有序链表：

      

    • 使用 mergeTwoLists 函数合并两个已排序的子链表，构建有序链表。
      • 

    

    4. 






复杂度





时间复杂度





    

  1. 递归深度：每次递归将链表长度减半，递归深度为\log n。
    2. 




  2. 每层操作：mergeTwoLists 函数需要遍历并合并两个子链表，耗时 O(n)。
    3. 




  3. 总复杂度为 O(n \log n)。
    4. 






空间复杂度





    

  • 递归调用占用的栈空间：由于递归深度为 \log n，因此空间复杂度为 O(\log n)。
    • 




  • 合并操作没有使用额外的空间，符合链表的原地操作特性。
    • 






方法二：

	


	
	
	
			

			
			Leetcode		

	





	

					暂无评论
			







	

		

			
			发送评论
			编辑评论
		

		
		

			

				

					
				

				

					

				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇

                    

                    
			        推荐文章
		            

		            

							
7.3 LeetCode 热题 100 (链表)

							
							

							
7.2 LeetCode 热题 100 (链表)

							
							

							
7.1 LeetCode 热题 100 (链表)

							
							

							
6.2 LeetCode 热题 100 (矩阵)

							
							

							
6.1 LeetCode 热题 100 (矩阵)