矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
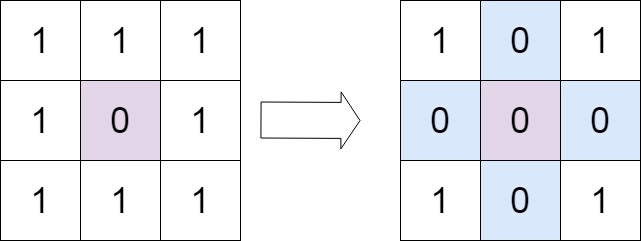
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
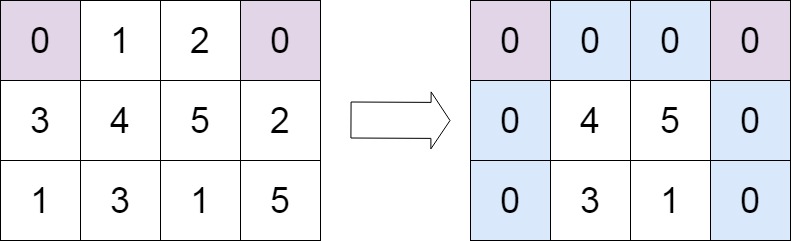
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
首次尝试
代码
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
col = []
row = []
m, n = len(matrix), len(matrix[0])
for i in range(m):
for j in range(n):
if matrix[i][j] == 0:
col.append(i)
row.append(j)
for i in range(m):
for j in range(n):
if i in col or j in row:
matrix[i][j] = 0总时间复杂度:$O(m \times n)$,这一点是符合题目要求的。
空间复杂度:使用了 col 和 row 两个列表存储需要置零的行和列。最坏情况下,如果矩阵中所有的元素都为零,这两个列表将分别包含 m 和 n 个元素。因此空间复杂度为$O(m + n)$,不符合题目要求的 常数级额外空间 $O(1)$。
改进
代码
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
m, n = len(matrix), len(matrix[0])
first_row_zero = False
first_col_zero = False
# Step 1: 标记第一行和第一列是否需要置零
for i in range(m):
if matrix[i][0] == 0:
first_col_zero = True
for j in range(n):
if matrix[0][j] == 0:
first_row_zero = True
# Step 2: 用第一行和第一列标记需要置零的行和列
for i in range(1, m):
for j in range(1, n):
if matrix[i][j] == 0:
matrix[i][0] = 0
matrix[0][j] = 0
# Step 3: 根据标记置零
for i in range(1, m):
for j in range(1, n):
if matrix[i][0] == 0 or matrix[0][j] == 0:
matrix[i][j] = 0
# Step 4: 处理第一行
if first_row_zero:
for j in range(n):
matrix[0][j] = 0
# Step 5: 处理第一列
if first_col_zero:
for i in range(m):
matrix[i][0] = 0优化后的复杂度分析
空间复杂度为 $O(1)$,满足题目要求。
时间复杂度:
初始标记 $O(m + n)$。
遍历矩阵进行标记 $O(m \times n)$。
根据标记置零 $O(m \times n)$。
总时间复杂度为 $O(m \times n)$。
空间复杂度:
只使用了两个布尔变量 first_row_zero 和 first_col_zero。
螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
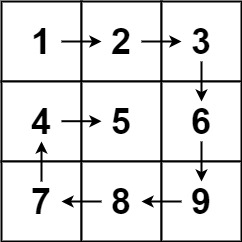
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
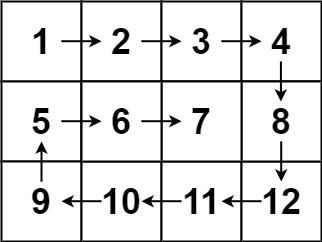
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
首次提交
提示
- 定义边界:
- 我们使用四个变量
top、bottom、left和right分别表示当前未遍历区域的上边界、下边界、左边界和右边界。 - 初始值为:
top = 0bottom = m - 1left = 0right = n - 1
- 我们使用四个变量
- 按照螺旋顺序遍历:
- 按照以下顺序遍历矩阵:
- 从左到右遍历当前的
top行; - 从上到下遍历当前的
right列; - 从右到左遍历当前的
bottom行(如果top <= bottom); - 从下到上遍历当前的
left列(如果left <= right)。
- 从左到右遍历当前的
- 每遍历完一条边后,收缩对应的边界(
top++、bottom--、left++或right--)。
- 按照以下顺序遍历矩阵:
- 结束条件:
- 当
top > bottom或left > right时,遍历结束。
- 当
代码
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m, n = len(matrix), len(matrix[0])
left, right, top, bottom = 0, n-1, 0, m-1
result = []
while True:
for i in range(left,right+1):
result.append(matrix[top][i])
top += 1
if top > bottom:
break
for j in range(top,bottom+1):
result.append(matrix[j][right])
right -= 1
if left > right:
break
for i in range(right,left-1,-1):
result.append(matrix[bottom][i])
bottom -= 1
if top > bottom:
break
for j in range(bottom, top-1, -1):
result.append(matrix[j][left])
left += 1
if left > right:
break
return result改进
代码
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m, n = len(matrix), len(matrix[0])
left, right, top, bottom = 0, n - 1, 0, m - 1
result = []
while left <= right and top <= bottom:
# 从左到右遍历当前的 top 行
for i in range(left, right + 1):
result.append(matrix[top][i])
top += 1
# 从上到下遍历当前的 right 列
for i in range(top, bottom + 1):
result.append(matrix[i][right])
right -= 1
# 从右到左遍历当前的 bottom 行
if top <= bottom: # 需要确保还有行
for i in range(right, left - 1, -1):
result.append(matrix[bottom][i])
bottom -= 1
# 从下到上遍历当前的 left 列
if left <= right: # 需要确保还有列
for i in range(bottom, top - 1, -1):
result.append(matrix[i][left])
left += 1
return result复杂度分析
- 时间复杂度:
- 遍历矩阵中的每个元素一次,时间复杂度为 O(m \times n)。
- 空间复杂度:
- 除了结果数组外,使用常数空间,空间复杂度为 O(1)。