环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
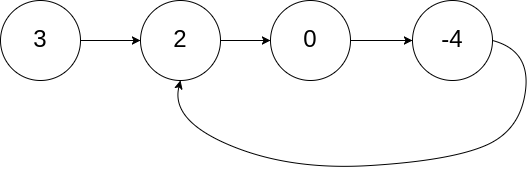
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
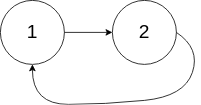
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
快慢指针
思路
- 使用两个指针(快指针
fast和慢指针slow)遍历链表:- 慢指针一次移动一步。
- 快指针一次移动两步。
- 如果链表中有环,快慢指针最终会在环中相遇。
- 如果链表中无环,快指针会先到达链表的末尾(
None)。
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
# 快慢指针初始化
slow = fast = head
# 检查初始条件
while fast and fast.next:
slow = slow.next # 慢指针走一步
fast = fast.next.next # 快指针走两步
# 快慢指针相遇,说明有环
if slow == fast:
return True
# 快指针或快指针的下一节点为 None,说明无环
return False复杂度
- 时间复杂度:
- 每次循环中,快指针和慢指针都向前移动,因此时间复杂度为 O(n),其中 n 是链表节点数。
- 空间复杂度:
- 仅使用了两个指针变量
slow和fast,空间复杂度为 O(1)。
- 仅使用了两个指针变量
环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
解法
思路
首先判断是否形成环,如果不是环则返回
如果是环则在维护一个指针从 head 开始与 slow 当前所在的位置同时开始移动,当他们俩个同时相遇时的Node就是环的第一个节点。
代码
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = fast = head
# 检测环的存在
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast: # 快慢指针相遇
break
else:
# 如果没有环,返回 None
return None
# 找入环点
fast = head
while fast != slow:
fast = fast.next
slow = slow.next
# 返回入环点
return fast复杂度
- 时间复杂度:
- 环检测:O(n),快慢指针每次移动后总共最多遍历链表一次。
- 入环点查找:O(n),再次遍历链表找到入环点。
- 总时间复杂度为 O(n)。
- 空间复杂度:
- 使用了常量级别的指针变量,空间复杂度为 O(1)。
分析总结
f 和 s分别表示快慢指针走过的距离,将可以形成环的链表使用a + b 来表示,其中a 为从head到环的第一个节点的距离,b 表示从环第一个节点到末尾的距离,从题中已知
$$
\left\{\begin{matrix} f=2s \\ f=s + nb \end{matrix}\right. \to \left\{\begin{matrix} s=nb \\ f=2nb \end{matrix}\right.
$$
同时我们可以将k表示为走到环的第一个节点时的距离:k = a + nb
因此我们可以得出:
$$
\left\{\begin{matrix} s=nb \\ k = a + nb \end{matrix}\right. \to k = s + a
$$
也就是当前的s再走a的长度就是环的第一个节点,同时a也是从链表head开始到环的第一个节点的距离。虽然我们不知道a的值是多少,但是我们从现在开始同时移动s和从链表head的指针,当他们相遇时所在的节点就是a。
合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
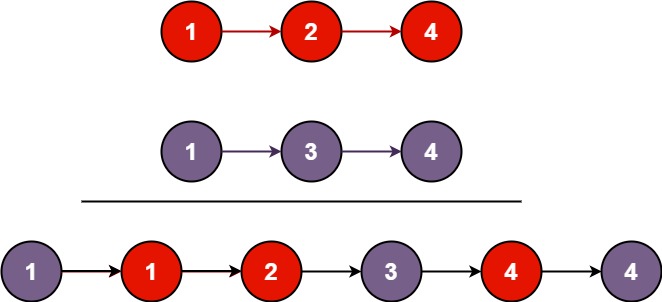
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
双指针解法
想法
- 创建一个哑节点
dum,用来简化链表的操作,同时定义一个cur指针用于跟踪新链表的尾部。 - 使用
while循环比较list1和list2的当前节点值,将较小的节点连接到新链表,并移动相应链表的指针。 - 当其中一个链表遍历完成后,将另一个链表的剩余部分直接连接到新链表的尾部。
- 最后返回
dum.next,即新链表的头节点。
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
# 创建哑节点,用于简化链表的操作
cur = dum = ListNode(0)
# 循环遍历两个链表,直到其中一个为空
while list1 and list2:
# 比较两个链表当前节点的值,选择较小的节点加入新链表
if list1.val < list2.val:
# 将 list1 当前节点加入新链表,并移动 list1 指针
cur.next, list1 = list1, list1.next
else:
# 将 list2 当前节点加入新链表,并移动 list2 指针
cur.next, list2 = list2, list2.next
cur = cur.next # 更新当前指针到新链表的最后一个节点
# 处理剩余的节点(当一个链表已经遍历完时)
# 如果 list1 剩余非空,则连接 list1;否则连接 list2
cur.next = list1 if list1 else list2
# 返回合并后的链表头节点(哑节点的 next)
return dum.next复杂度分析
- 时间复杂度:
O(m + n),其中m和n分别是list1和list2的长度。需要遍历两个链表的所有节点一次。
- 空间复杂度:
O(1),因为没有使用额外的空间,仅使用了常数个变量
递归解法
两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
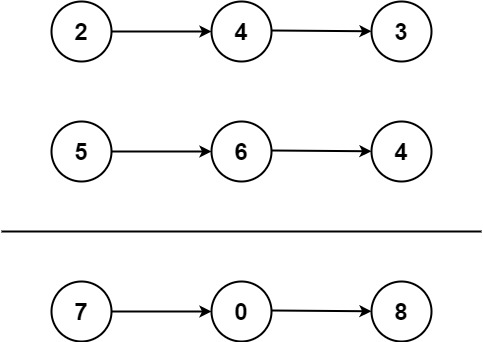
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
方法
代码逻辑
- 哑节点初始化:
- 使用
dum简化链表的操作,避免处理特殊头节点。 cur用于指向当前新链表的最后一个节点。
- 使用
- 主循环逻辑:
- 遍历两个链表,将其值与进位
carry相加。 - 计算当前节点值和新的进位,创建新节点存储结果。
- 使用条件判断处理链表节点为空的情况,默认值为
0。 - 将
carry的逻辑纳入主循环中,避免遗漏尾部进位的情况。
- 遍历两个链表,将其值与进位
代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
# 创建哑节点简化操作
cur = dum = ListNode(0)
carry = 0 # 初始化进位
# 遍历两个链表,直到两者都为空
while l1 or l2 or carry:
# 获取当前节点的值,如果链表为空则为0
val1 = l1.val if l1 else 0
val2 = l2.val if l2 else 0
# 计算总和以及新的进位
total = val1 + val2 + carry
carry = total // 10
cur.next = ListNode(total % 10) # 新节点存储当前位的值
# 移动链表指针
cur = cur.next
if l1: l1 = l1.next
if l2: l2 = l2.next
# 返回结果链表(哑节点的 next)
return dum.next
复杂度分析
- 时间复杂度:
O(max(m, n)),其中m和n分别是l1和l2的长度。
- 空间复杂度:
O(1),仅使用了常数空间(进位变量和几个指针)。
简洁版注意事项总结如下:
注意事项
- 链表长度不同:
- 使用
val1 = l1.val if l1 else 0处理短链表,避免动态扩展。
- 使用
- 进位处理:
- 使用
carry存储进位,计算方式为carry, value = divmod(val1 + val2 + carry, 10)。 - 循环结束后若
carry > 0,添加额外节点。
- 使用
- 哑节点技巧:
- 用哑节点
dum简化链表操作,返回时直接用dum.next。
- 用哑节点
- 测试边界条件:
- 两链表长度不等。
- 一个链表为空。
- 最后进位。
