括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
**输入:**n = 3
**输出:**["((()))","(()())","(())()","()(())","()()()"]
示例 2:
**输入:**n = 1
**输出:**["()"]
思路
使用 回溯算法(Backtracking) ,递归构建所有合法的括号字符串。我们从空字符串出发,每一步选择加 '(' 或 ')':
- 加左括号的条件:当前已加的左括号数量
< n; - 加右括号的条件:当前已加的右括号数量
< 当前左括号数量(确保字符串合法); - 当左右括号都用完(即
left == right == n)时,将当前构造的字符串加入结果列表。
采用 DFS 深度优先遍历方式,每次递归都尝试加 '(' 和 ')',并进行合法性剪枝。
Code
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
output = [] # 存储所有合法结果
temp = [] # 当前构建中的括号组合
def dfs(left: int, right: int, temp: List[str]):
# 如果左右括号都用完了,加入结果
if left == right == n:
output.append(''.join(temp))
return
# 如果左括号还没用完,可以加左括号
if left < n:
temp.append('(')
dfs(left + 1, right, temp)
temp.pop() # 回溯
# 如果右括号数量小于左括号,才可以加右括号
if right < left:
temp.append(')')
dfs(left, right + 1, temp)
temp.pop() # 回溯
dfs(0, 0, temp)
return output
时间空间复杂度
- 时间复杂度:$O(\dfrac{4^n}{\sqrt{n}})$
每个有效括号组合是卡特兰数 $C_n $,即 $\dfrac{1}{n+1} \binom{2n}{n}$,近似 $O(\dfrac{4^n}{\sqrt{n}})$; - 空间复杂度:$O(n)$,递归栈最大深度为 $2n$,但当前路径最多存储 $n$ 个左括号。
注意事项
- 回溯法中一定要在递归前
append(),递归后pop(),维护当前路径; - 加右括号必须满足
right < left; - 不要在加括号时嵌套条件判断,保持两个 if 分开。
错误反思
- 初版代码未对
temp 添加括号字符,仅递归了参数; - 右括号的添加条件写在了左括号的判断内部,导致当左括号耗尽时右括号逻辑被跳过;
-
temp.pop() 只调用了一次,而可能append() 了两次,造成回溯不完整。
关键点
- 使用递归构造所有合法组合;
- 明确添加
'(' 和')' 的条件; - 每一步都要做回溯撤销操作,避免影响其他分支。
单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
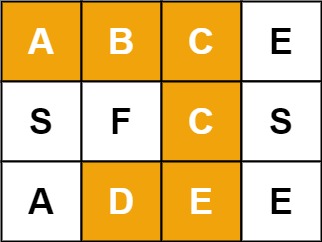
输入:
board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"输出:
true
示例 2:
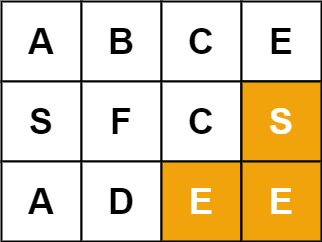
输入:
board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"输出:
true
示例 3:

输入:
board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"输出:
false
思路
使用 回溯算法 + 深度优先搜索(DFS) 来在二维字符矩阵中查找目标单词 word 是否存在。
搜索规则:
- 单词必须按照字母顺序逐个匹配;
- 每个字母必须来自当前格子的上下左右邻接格子;
- 每个格子中的字母只能使用一次。
解法步骤:
- 遍历所有格子,以每个格子为起点;
- 进行 DFS 搜索;
- 如果路径匹配成功,返回
True; - 使用
visited 记录访问状态,防止重复使用; - 回溯时要取消访问标记(即恢复现场)。
Code
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
m, n = len(board), len(board[0])
visited = [[0] * n for _ in range(m)]
def dfs(x, y, i):
# 剪枝:当前字符不匹配或已经访问过
if board[x][y] != word[i] or visited[x][y] == 1:
return False
# 如果已经匹配到最后一个字符
if i == len(word) - 1:
return True
visited[x][y] = 1 # 标记当前格子已访问
res = False
# 遍历四个方向
if x > 0 and dfs(x - 1, y, i + 1): res = True
if x < m - 1 and dfs(x + 1, y, i + 1): res = True
if y > 0 and dfs(x, y - 1, i + 1): res = True
if y < n - 1 and dfs(x, y + 1, i + 1): res = True
visited[x][y] = 0 # 回溯
return res
# 遍历所有起点
for i in range(m):
for j in range(n):
if dfs(i, j, 0):
return True
return False
时间空间复杂度
-
时间复杂度:$O(m \cdot n \cdot 3^L)$,其中 $L$ 是
word 的长度;- 最多从 $m \cdot n$ 个起点出发,每次最多递归 3 个方向(不走回头路);
-
空间复杂度:$O(m \cdot n)$,用于记录
visited 状态;- 递归深度最多为
L,所以额外栈空间为 $O(L)$。
- 递归深度最多为
注意事项
- 判断边界时要确保下一个坐标不越界,而不是判断当前;
- 必须在每次 DFS 结束后回溯(即
visited[x][y] = 0),否则状态会残留; - 若提前
return 而未执行回溯,会导致错误路径干扰正确解。
错误反思
- 错误地将边界判断写成
x >= 0 而不是x > 0; - 使用
i += 1 导致路径共享变量修改,造成逻辑错误; - 忘记回溯访问状态,导致部分路径无法复用格子;
- 分支中使用
return 而不是收集res,导致提前退出、回溯未执行。